Lecture 19
上一节定义了非常多的定义,这一节将会讲三个例子进行验证。
上一节引出的定义subgame perfection,就是为了将同时博弈和线性博弈进行融合,填补他们之间的隔阂。
第一个游戏
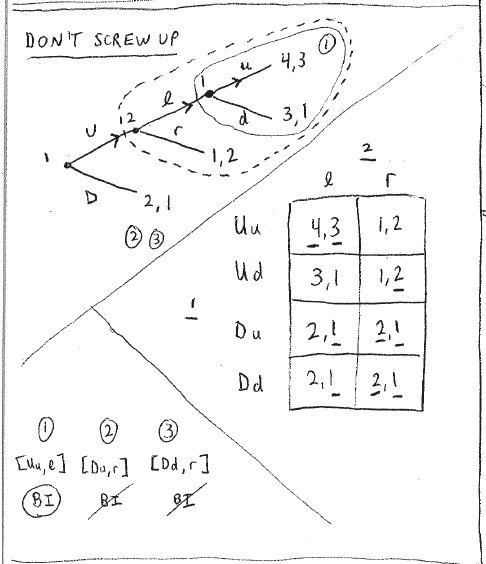
这个游戏能够找到3个NE(Nash Equilibrium),但是只有一个SPE(subgame perfect NE)。并且仅有的的这一个是符合BI(back induction)推导的。
matchmaker game
三个玩家的游戏,玩家1尝试着撮合玩家2和玩家3当成某项共识。
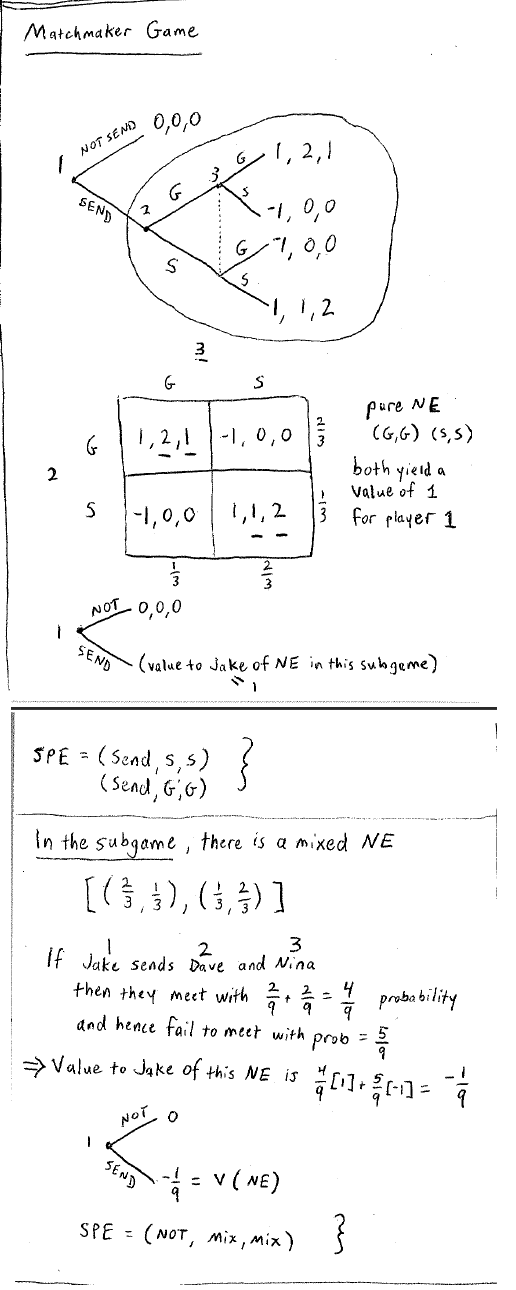
混合策略下的概率,之前已经推导过了第一个玩家选择(G, S)的概率为(2/3, 1/3);同理玩家2选择(G, S)的概率为(1/3, 2/3)。
这个游戏通过推导可以看出pure strategy有两个SPE,混合策略情况下也有SPE。
strategic investment
在Lecture 6中,我们已经讨论了两个玩家,进行古诺博弈。
先进行一些简单的复习:
商品的价格是根据来决定的。
假设现在的边际成本是 $1M/t
根据lecture 6中的计算结果,如果最后达到纳什均衡,那么最后的产量
因此最后的
每一个公司的利润为
现在有一台新的机器:
- 仅能被A使用
- 费用 $0.7 M/年
- 能够降低A的生产成本$0.5 M/吨
问题:要不要租赁该机器?
会计的答案
每一年生产量为1,因此节约的成本0.5<0.7,因此不租赁。
经济学答案
会计的计算的产量是错误的,因为一旦价格变化了,那么产量就会变化,也需要将产量的变价计算其中。
如果计算变化的产量,通过价格-需求曲线进行计算:
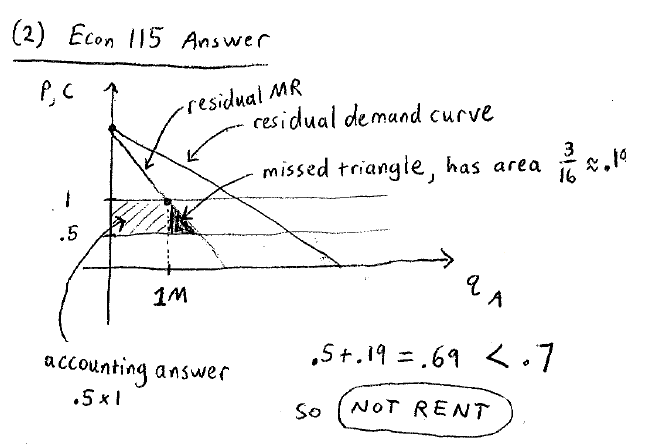
博弈论的答案
通过最佳对策曲线进行决策:
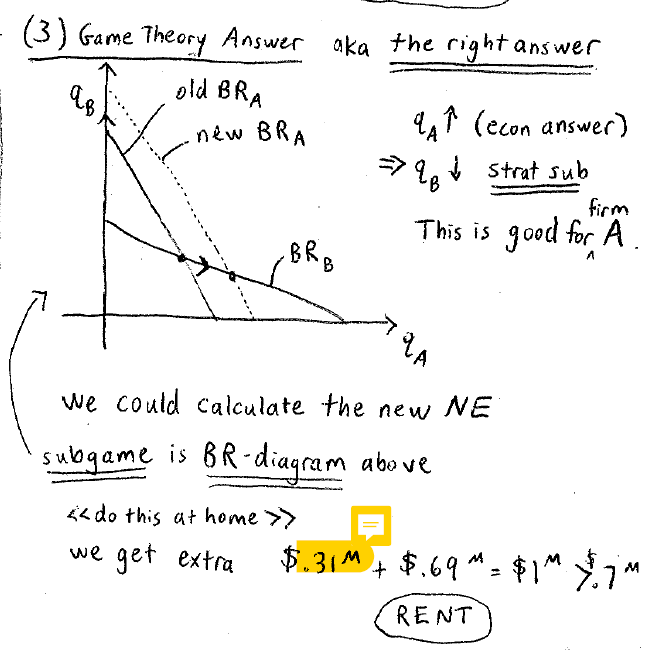
在这个博弈中,不仅有商品价格下降带来的产量的增加,还有对手减产自己产量的增加,一共有两部分的增加。
- 通过计算子游戏的收益,然后进行回代。
- 不要忘记对手变化对自己的影响。